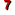It is not the question how synthetical judgments are possible, which would be a psychological question, but how synthetical propositions can be true and be known to be true. But I shall not make his division of propositions into the a priori and the a posteriori the leading one, but rather the division into derived and ultimate propositions. We must be on our guard in defining this distinction not to fall into a mere matter of psychology, as Kant does, floundering in a muddy bog of land and water, a psychological deduction and a "transcendental" deduction mixed. By an ultimate premiss we must understand a proposition not derived by an ascertainably self-controlled logical process. We need not assume that there is any premiss over whose derivation it is impossible to exercise any control. It will suffice that, in fact, as far as we have ascertained, there has been no such control. Derived propositions are justified by the arguments by which they are derivable; and the justification of such arguments will be considered in subsequent memoirs. In regard to underived propositions, we may for the moment compare a man who makes a judgment with a piece of paper on which a proposition is written. If somebody has idly written on a piece of paper, `The moon is made of green cheese', he has not made himself responsible for the truth of the proposition; and if it were asked how the paper was justified for carrying such a lie, the obviously sufficient answer would be it cannot help it. In like manner if a man looks at the moon and judges that it looks bright, this judgment is entirely unlike the percept from which it is derived, and still more unlike the first impressions of sense. Still, we have no need of following Kant in attempting to make out what the psychological process is. No use could be made of such knowledge, if we had it, and Kant's psychological deduction is manifestly idle. The one perfectly sufficient justification is that the man can no more help judging that the moon he is looking at seems bright than a piece of paper can help what is written upon it. For who is to find fault with him? As long as he keeps his opinion to himself, as long as he cannot help believing that the moon looks bright, he does believe it perfectly; and as long as he does believe it perfectly, he does not in the least doubt it, and as long as he cannot help believing it, he cannot doubt it. In short it appears to him evidently true; and he cannot blame himself for believing what is manifestly true. He cannot so much as make an effort to believe otherwise. "So, then," somebody may say, "you believe in the test of inconceivability." But nobody has any right to draw such an inference. On the contrary, it is fairly presumable that I am consistent in my opinions; and consistency with what I have just been saying forces me to declare, not indeed that the test of inconceivability is untrustworthy, but that the phrase `test of inconceivability' is a self-contradictory jumble of words, and that nobody can either trust to it or distrust it, since there is no such thing. If a man cannot help entirely believing that a proposition is true, it is absurd for him to pretend that his not being able to doubt it is his reason for believing it. He has no reason whatever for believing it; for reasoning is essentially self-controlled, while he cannot help believing it. A reason is only operative while a man is changing his mind. When he is once convinced, we say he has a reason for his belief; but that only means that he can imagine himself to be oblivious of the reason and to doubt the proposition and that he sees, or thinks he sees, that if that were the case, the knowledge of the reason would silence his doubts. Strictly speaking, he is not now under the influence of the reason; and he "has" a reason for his belief only in the sense of having stored in his mind something which he feels would act as a reason should he ever be led to doubt the proposition. A man has no reason for what he does not doubt, still less any such ridiculous reason as that he does not doubt it. I know that it may be said that the test of inability to doubt is one thing and the test of inability to conceive is another. But I deny it. What those people mean who talk of the test of inconceivability [i.e. what this] means to them [is] simply erecting inability to doubt into a reason. It is true that their minds are in a confused state, as their language shows. It will be shown that true inconceivability can only arise as a consequence of what is called self-contradiction. But many things are said by logically untrained minds to be inconceivable because they seem to them so strange that they do not know how to go to work to frame the conception. For example, many persons would say that a man's being the father of his own father was inconceivable. But there are various ways in which such an event may be conceived, as, for example, by simply supposing that all time forms a closed cycle which the two lives completely exhaust. Certainly, unless there is some abstruse reason to the contrary which does not at once strike me, it is quite possible that, as a matter of fact, time does form a closed cycle. At the same time, until some positive reason shall appear for believing that it is so, it will be shown in another memoir that we are justified in disbelieving it; and it is simply because they cannot entertain a doubt on the subject, that some people pronounce the idea inconceivable; unless they are dominated by the narrowest associations of ideas.

      Now what are the things which cannot be doubted? I will begin by abandoning the field of pure logic, and asking what are the things that I personally, find I cannot doubt. Doubt may be present in very slight degree. Suppose there are a thousand propositions that, as far as I can see, I do not, in fact, in the least doubt. Still, I might think viewing them collectively, that some one of them, I know not which, may be erroneous. I certainly do believe that among all the opinions which I most firmly hold there are errors, very likely a good many errors. This could not be if I had not the smallest doubt of any one of them. There are doubts, then, in my mind which are so faint that with all the energy of attention which I can well bestow upon the scrutiny of my state of mind, I am not able to discern. But if there by anything that I do not doubt at all, it must be a proposition the evidence for which presents itself in its entirety here and now. For although a compulsion may conform to a general law, it cannot have any mode of being other than that of direct activity here and now. It can, therefore, be no general proposition. It must be a perceptual judgment; that is, the judgment that a present percept has a certain appearance.

      At the same time, I cannot, by a mental operation, doubt anything which I do not already doubt. I do not mean to deny that a surprising experience might create doubts not previously existing. I cannot even review the evidence for a belief, unless I entertain a doubt of it. Moreover, every doubt which I entertain is founded upon some reason for a contrary belief. But when, in consequence of a slight doubt, founded, perhaps, upon no more definite reason than that I have often found myself mistaken, I am led to reexamine the evidence, it very frequently happens that I discover some circumstance which creates a doubt very much stronger, and founded upon altogether different reasons.

      Passing now to the pure logical doctrine, an assertion is an act which represents that an icon represents the object of an index. Thus, in the assertion, `Mary is red-headed', `red-headed' is not an icon itself, it is true, but a symbol. But its interpretant is an icon, a sort of composite photograph of all the red-headed persons one has seen. `Mary' in like manner, is interpreted by a sort of composite memory of all the occasions which forced my attention upon that girl. The putting of these together makes another index which has a force tending to make the icon an index of Mary. This act of force belongs to the second category, and as such, has a degree of intensity. Not that degree in itself belongs to the second category. On the contrary, it belongs to the third. Degree is not a reaction, or effort, but a thought. But degree attaches to every reaction. Consequently, every assertion has a degree of energy.

      Either at this point or later in the memoir, I shall examine the so-called tests [of] universality and necessity which are supposed to prove the a priori character of certain propositions. I shall first trace the history of this doctrine. I shall then show that the statement of it is incomplete, there being a number of other characters which are equally entitled to be considered as tests of apriority. I shall then show that there are two senses in which the test has been understood; and that there is a third sense which makes a more defensible doctrine than either. I show that the test may be understood to embody several logical truths; yet if any proposition is universal, necessary, etc., and there is nothing to show that it is true, the only logical position is that it is false. A first premiss, other than a fact of perception, is inadmissible. Kant's position is that it is easy to show by universality and necessity that certain propositions are a priori, but that their truth remains to be proved by an abstruse line of reasoning. Now it would [be] absurd to admit into that reasoning any a priori proposition as long as one maintains that such reasoning is necessary to support any a priori proposition; and in fact Kant's premisses appear to be quite evidently generalizations of common experience. But granting that he in this way proves the truth of an a priori proposition, it follows that antecedently to this proof it was an idle hypothesis, and that its only support is a purely experiential argument. But that is pure positivism; and Kant's doctrine really seems to be nothing but nominalistic sensualism so disguised that it does not recognize itself. Of course, it may be said that Kant only maintains the concepts, not the judgments, to be a priori. In the first place, this is directly contrary to Kant's own opinions. In the next place, universality and necessity are characters of propositions, not of terms. In the third place, Hume himself, even as Kant misrepresents him, [and] much more [i.e., and all the more] in his true character, would have been ready to admit that some forms of thought arise from the nature of mind. Some persons who have believed themselves to be Kantians hold that as soon as a proposition is shown to be a priori, it is beyond all criticism. That is utterly contrary to the spirit of Kant. But it is quite true that if there is anything which I cannot help believing without any tincture of doubt, I am out of all real discussion of its truth. No doubt that for many persons there are such propositions, if by doubt we mean any doubt that they recognize; and if by `can', we refer to ability conditioned upon such means as they have put into practice. Propositions so believed are almost always false; but there is no way for their victims to be undeceived as long as they cherish that state of mind. This seems to be the state of all those persons who think that philosophy and logic are idle things; that all that is required is a little good sense and reflection, and that extensive reading and study are useless.

      The previous memoir, No. 20, will have contained an elaborate analysis of the logical nature of doubt which will be applied to the problems of the present memoir, especially to show that judgments founded on the experience of every hour of every man's life are not subject to doubt of the ordinary kind and have some of the characteristics attributed to a priori propositions.

      Other views will be critically examined.

---

 

Final Version - MS L75.373-375

MEMOIR   22

THE LOGIC OF CHANCE

      I here discuss the origin and nature of probability by my usual method; also the connection between objective probability and doubt; the nature of a "long run"; in what sense there can be any probability in the mathematical world; the application of probability to the theory of numbers. I show that it is not necessary that there should be any definite probability that a given generic event should have a given specific determination. It is easy to specify cases where there would be none. There appears to be no definite probability of a witness's telling the truth. I also show that it is quite a mistake to suppose that, for the purposes of the doctrine of chances, it suffices to suppose that the events in question are subject to unknown laws. On the contrary, the calculus of probability has no sense at all unless it in the long run secures the person who trusts to it. Now this it will do only if there is no law, known or unknown, of a certain description. The person who is to trust to the calculus ought to assure himself of this, especially when events are assumed to be independent. The doctrine of chances is easily seen to be applicable in the course of science. Its applicability to insurance companies and the like is not in any case to be assumed off-hand. When it comes to the case of individual interests, there are grave difficulties.

      The rules of probability are stated in a new way, with the application of high numbers and method of least squares according to several different theories. Pearson's developments examined. Inverse probabilities are shown to be fallacious.

      There are many matters here under dispute; more than I here set down. In all these cases, I take pains to state opposing arguments in all their force, and to refute them clearly. This memoir is intended to form a complete vade mecum of the doctrine of chances, and to be plentifully supplied with references. It will be somewhat long, but I hope not of double length.

From Draft D - MS L75.263-268

      Deduction, as such, is not amenable to critic; for it is necessary reasoning, and as such renders its conclusions evident. Now it is idle to seek any justification of what is evident. It cannot be rendered more than evident. Fallacies, it is true, may be criticized; but this subject will be postponed until all the legitimate modes of argument have been considered.

      But when deduction relates to probability, it becomes open to criticism, not insofar as it is deductive but insofar as it relates to a logical conception which in a sense deprives the reasoning of its necessary character. I therefore in this memoir examine the nature of probability, and the processes of the doctrine of chance. I flatter myself that I shall put the whole matter, both of the origin of probability and of the application of the calculus, in a much clearer light than has hitherto been done. Objective probability is simply a statistical ratio. But, besides that, doubt has degrees of intensity, and although these have no necessary signification, it might be useful for us to believe more intensely in propositions which would less often deceive us than in such as would oftener deceive us. In point of fact, we naturally "weigh" or "balance reasons," as if the degree of our trust in them were significant of fact. This is a matter requiring minute examination.

      In the first place, regarding probabilities as statistical ratios, probability is exclusively confined to cases where there is a "long run" of experience, that is, an endless series of events of a general character, of which some definite ratio have a special character, which shall not occur at any regular law of intervals. It is not necessary that this ratio should remain constant throughout the experience. But it is requisite that there should be such a ratio. It is easy to imagine cases in which there should be no such ratio; perhaps even a universe in which there should be no such thing as probability. (I will endeavor to determine this with certainty before drawing up the memoir.) It is commonly said that there is a law of the occurrence of the event, only it is unknown to us. But it is easy to show that the utility of the calculus depends on there being no law of the kind which would concern the application. Ignorance is not sufficient.

      The rules of probability are easily deduced, involving the conception of independent events, that is, events such that the product of the number of occurrences of both into the number of non-occurrences of both equals the product of the number of occurrences of the first only into the number of occurrences of the second only. From this follows the probability law.

      Now as concerns the connection between probability and doubt, we find the books stuffed with errors. It is, for example, generally said that probability 1 represents absolute certainty. But on the contrary, probability 1 is that of an event which in the entire long run fails to occur only a finite number of times. In the next place, the majority of the books give formulae from which it would follow that the probability of a wholly unknown event is 1/2. It is evident that probability, in this crude form, is quite unadapted to expressing the state of knowledge generally. The relation of real evidence to a positive conclusion is not a mathematical function. From a bag of beans, I take out a handful, in order to test a theory which I have some other reason for entertaining, that two thirds of the beans in the bag are black. I find this to be nearly so in the handful, and my theory is confirmed, and I now have strong reason for believing it approximately true. But it is not true that there is any definite probability that it is true. For what would such a ratio mean? Would it mean that once in so often my conclusion is true? That depends on the general commonness of different distributions of beans in a bag, which is a positive fact, not a mathematical function. Mathematical calculation is deductive reasoning, applicable solely to hypotheses; and whenever it is applied to do the work of induction or abduction it is utterly fallacious. This is an important general maxim.

      This consideration affects the method of least squares, if this method is looked upon in an extravagant theoretical manner; but not if it is regarded as a way of formulating roughly an inductive inference. Mr. Pearson's extensions, though they are excessively complicated, and thereby violate the very idea of least squares, are not without value. but other somewhat similar modifications of probability are called for; and I shall endeavor to work out one or two of them.

      I give in this memoir a summary of all the ordinary scientific man needs to know about probability in a brief intelligible manner. It will have the advantage over Bertrand's book of being sound.

From Draft D - MS L75.311-312

      Although deduction is not directly and as such amenable to critic, yet it becomes such when it deals with probability and certain allied conceptions. The criticism is not properly of the deductive process but of those conceptions. I here examine the philosophy of probability and show, among other things, that it is by no means true that every contingent event has any definite probability. I describe the construction of an urn of black and white balls such that there is no definite probability that a ball drawn will be white. By way of illustration, I show that there is no definite probability that a witness will tell the truth. Another point I make clear is the distinction between probability unity and certainty. This is illustrated by the case where a large number of players, playing against a banker, at a perfectly even game, each bet one franc each time until his [bet] nets a gain, when he retires from the table and gives place to a fresh player. The probability is 1 that any given player will ultimately net a gain, and therefore that all will do so; and yet the probability is 1 that in the long run the bank will not lose, or at any rate, there is an even chance that if the banker does not come out precisely even he will win, too. I show that the "moral value" of a player's chances is quite irrelevant to the Petersburg paradox; and I correct various other errors current about probability. Hume's argument about miracles will be analyzed.

      Rules by which all errors in the use of the doctrine of chances [can be identified] will be plainly laid down, and their use exemplified.

---

 

Final Version - MS L75.375

MEMOIR   23

ON THE VALIDITY OF INDUCTION

This restates the substance of the Johns Hopkins paper: relegating formalistic matters to separate sections, taking account of types of induction with which I was not acquainted twenty years ago, and rendering the whole more luminous. Other views will be considered more at large.

From Draft E - MS L75.176

      This memoir will repeat substantially the theory of induction given in my paper in the John Hopkins Studies in Logic, but now stated in essential points more fully and clearly, while formalistic matters are relegated to special sections. Moreover, my subsequent discovery of forms of induction quite different from any there considered, to which the applicability of the rules there developed is not evident, renders a new presentation necessary. I shall now consider other views more fully, and illustrate the bad influence they have had upon science.

From Draft D - MS L75.268-270

      It will be shown to be mathematically impossible that induction indefinitely persisted in should ultimately lead to a false conclusion in any case whatsoever, whether there be any definite probability or not, whether there be any real universe or not, whether the universe be presided over by a malign power bent upon making inductions go wrong or not. Such things might prevent inductions from being drawn, but they could not make them go ultimately wrong if they were rightly conducted and sufficiently persisted in. From this principle follow certain rules of induction for each of the three types of induction. These rules are clearly formulated and illustrated historically.

      I then proceed to inquire how far inductions may be strengthened or weakened by other arguments, which do not in themselves afford any information concerning the subjects of inquiry in the inductions, but which do give information strengthening or weakening any conclusions obtained. In particular, I show that the knowledge of certain uniformities (of which four types are the simplest) may so affect inductions.

      I now review all the other theories of induction, beginning with that of LaPlace which undertakes to assign a definite probability to the inductive conclusion. I show that that is erroneous, and that, rightly applied, Laplace's method would lead to the result that we know nothing about the truth of the conclusion. I next examine those theories that the future is like the past, that the universe presents great uniformity, and demonstrate that assuming those premisses to be true, they do not in the least help the validity of induction. I show that all such statements really mean nothing except that a badly conducted induction will lead to the truth, and that they are not true. The question of whether there is any objective sense in which they are true will be postponed to a separate memoir. I go on to consider several other theories of induction which mostly amount to denying its validity.

From Draft A - MS L75.39-42

      The doctrine commonly held that the validity of induction depends upon the uniformity of nature, or what comes to the same thing, upon the resemblance of the future to the past, is erroneous. I find that there are no less than eight incompatible ideas of what the uniformity of nature consists in, which not only have been put forward, but are widely current. But the doctrine is false in every sense. The most usual meaning attached to whichever of the two phrases happens to approve itself is really nothing but a dimly apprehended notion that some one of the lower forms of induction is valid reasoning. This will be proved incontestably in my book. Now it is nonsense to say that the validity of induction depends upon itself; and it is false that the validity of the highest forms depends solely on that of any lower form. Consequently, the doctrine, as ordinarily held, is nothing but a twist of language by which the validity of some kind of induction is restated in other words. If any of the other seven meanings is attached to the phrase `the uniformity of nature', there is no difficulty in supposing a world which should not present that uniformity. Now two of the meanings attached to the phrase are such that in a world without uniformity no induction, good or bad, could be drawn. In such a world, there could be no experience, properly speaking, and no reasoning of any kind. But the moment one supposes the universe to be such that a false induction becomes possible, I prove by mathematical demonstration that pure induction has all the validity that it has in the actual universe, although it cannot, perhaps, be fortified by the discovery of special uniformities. But an argument from a uniformity is not inductive; it is a deduction going to fortify an induction which is made a matter of observation.

      The thought may suggest itself[,] that the question whether the validity of induction rests on the uniformity of nature or what[,] is a somewhat idle one, of no practical importance. But such an opinion will be retracted by a reasonable man as soon as he learns, as my book will prove beyond possible dispute, that from my doctrine of the validity of induction it follows necessarily that certain rules and precautions ought to be observed in the practice of induction, at the peril of great mistakes, which rules and precautions are habitually disregarded by all but the keenest and most careful reasoners. My doctrine makes the security of induction wholly depend upon the honesty and skill of the inquirer. The other doctrine throws off all responsibility and puts it upon the broad shoulders of Nature. The consequence is that these logical treatises which rest the validity of induction upon a special constitution of nature have no reason for insisting and in fact do not point out at all the essential precautions which are as indispensable to the security of the proceeding as they are usually neglected.

---

End of PART 7 of 10 of MS L75

---